
백트래킹 알고리즘 백준 15649 N과 M
문제 링크

백트래킹을 이해하는 기본적인 알고리즘이다. 백트래킹 알고리즘이란 모든 경우의 수를 모두 고려하는 알고리즘이다. 문제를 트리 구조로 표현할 때 적합한 방식이다. 구현하는 방식에 따라 DFS, BFS로 구분될 수 있다. 문제에서 출력값을 사전 순으로 출력해야 하기에 BFS보다는 DFS 알고리즘을 사용하는게 맞다. DFS 알고리즘과 백트래킹의 차이점은 DFS는 리프노드까지 무조건 탐색을 진행하지만 백트래킹은 특정 조건값을 통해 복귀 로직이 포함된다.
DFS는 루트 노드에서 리프 노드까지 한번에 내려가는 방식이다. 예를 들어 미로 길 찾기 문제에서 막다른길 까지 도달한 후 길이 막히는 경우 원점으로 돌아와서 다시 길을 찾아나가는 방식이다. BFS 보다는 시간이 오래걸릴 수 있고 심지어 길을 아예 찾지 못할 수도 있지만 이번 경우에는 DFS 알고리즘을 사용하는게 맞다.
예를 들어 N = 3, M = 3이 주어지는 출력의 경우의 수를 트리로 도식화하면 다음과 같다. 최초 요소를 시작으로 가능한 모든 경우의 수를 구하기 위해 leaf node까지 내려가서 조사하는 방식이기 때문에 DFS로 해당 출력값을 구해낼 수 있다. DFS 알고리즘은 재귀 함수를 사용한다.
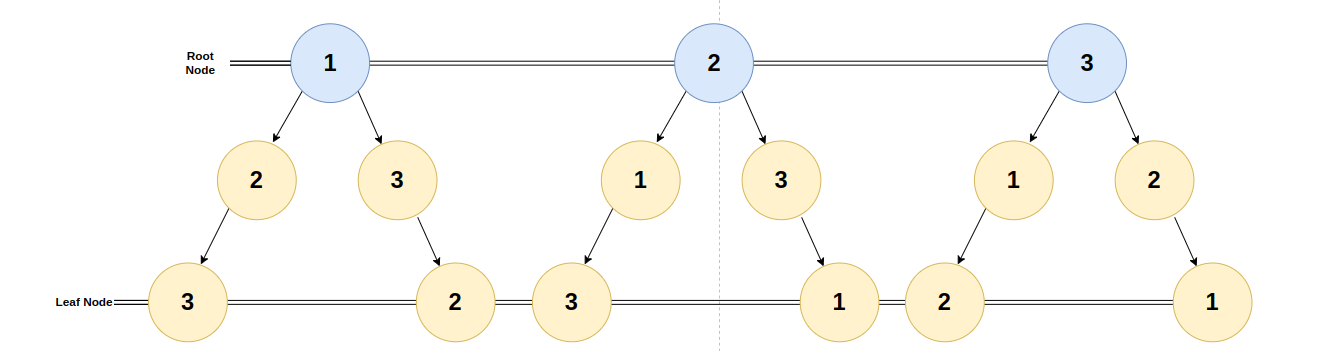
백트래킹 알고리즘은 발생할 수 있는 경우의 수를 구할 때 막다른 길(조건값)에 도달하는 경우 이전 단계로 복귀해야 한다. 문제에서 주어진 조건값은 중복없이 출력값을 구해내야 하기 때문에 1,2,1에 도달하는 경우 조건값에 맞지 않기 때문에 상위 노드로 복귀 해야 한다.

먼저 입력값을 배열 형태로 입력 받는다.
const N = input[0];
const M = input[1];
const result = [];
백트래킹 재귀함수를 구현한다.
const DFS = ()=>{
if(result.length == M) {
console.log(result.join(' '));
return;
}
for(let i=1; i<=N; i++){
if(!result.includes(i)){
result.push(i); // 요소를 추가한다.
DFS(); // 하위 노드로 이동한다.
result.pop(); // 이전 노드로 복귀한다.
}
}
}
재귀 함수가 호출되는 과정
함수가 한번 호출되는 경우 (----)가 붙는다.
ex) N = 3, M = 2
push(1) // result = [1]
----push(2) // result = [1, 2]
--------console.log(result.join(' '));
----result.pop() // result = [1]
----push(3) // result = [1, 3]
--------console.log(result.join(' '));
----result.pop() // result = [1]
result.pop() // result = []
result.push(2) // result = [2]
----result.push(1) // result = [2, 1]
--------console.log(result.join(' '))
----result.pop() // resut = [2]
----result.push(3) // result = [2, 3]
--------console.log(result.join(' '))
----result.pop() // result = [2]
result.pop() // result = []
result.push(3) // result = [3]
----result.push(1) // result = [3, 1]
--------console.log(result.join(' '))
----result.pop() // result = [3]
----result.push(2) // result = [3, 2]
--------console.log(result.join(' '))
----result.pop() // result = [3]
result.pop() // result = []
Javascript 백트래킹 소스 코드
/*
문제 : 백준 수 백트래킹 입문 1
날짜 : 2022-06-11
작성 : About-Tech
*/
const readline = require('readline');
const { stdin : input, stdout : output } = require('process');
const rl = readline.createInterface({input, output});
rl.on('line', (line)=>{
const input = line.split(' ');
const N = input[0];
const M = input[1];
const result = [];
const DFS = ()=>{
if(result.length == M) {
console.log(result.join(' '));
return;
}
for(let i=1; i<=N; i++){
if(!result.includes(i)){
result.push(i);
DFS();
result.pop();
}
}
}
DFS();
rl.close();
})
rl.on('close',()=>{
process.exit();
})
소스는 간단한데 재귀함수를 사용하고, 특정 조건값을 걸어 복귀를 해야하는 로직이 포함되야 하기 때문에 구현하기가 쉽지만은 않다. 미로탐색이나 DFS 심화 알고리즘에 사용되므로, 기본적인 백트래킹 코드는 충분히 이해하고 있을 필요가 있다.

백준 15650 JS 구현
N과 M 문제 시리즈 2번이다.
문제 링크
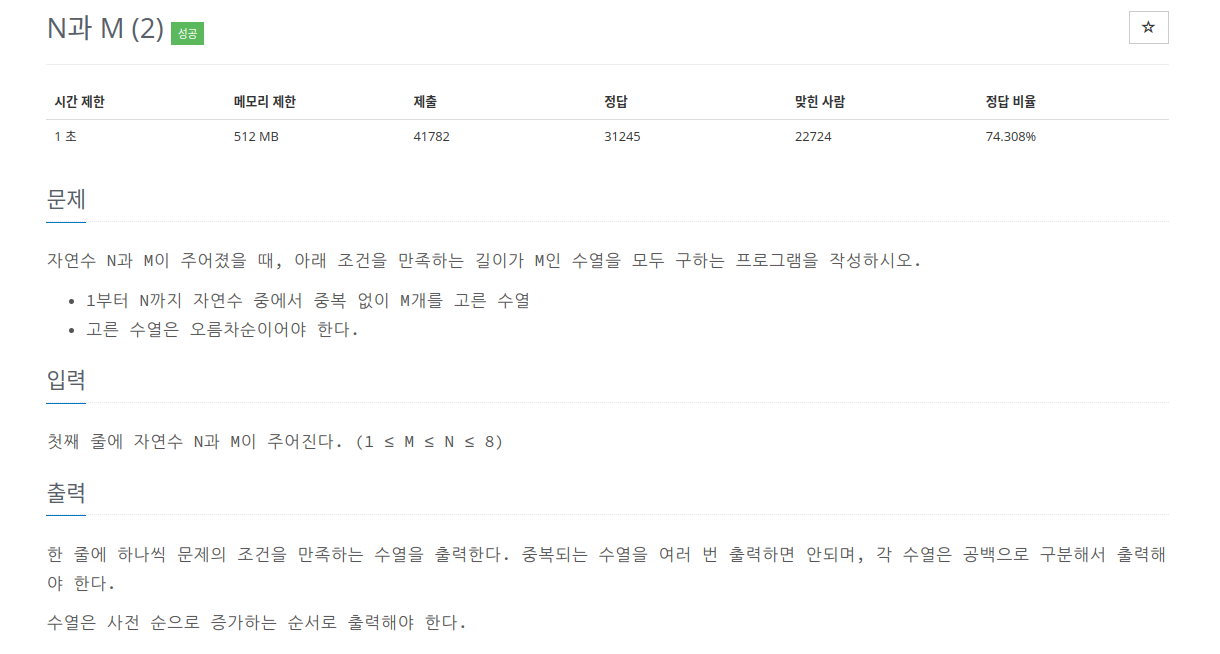
백준 15649번의 경우 가능한 모든 경우의 수를 출력하지만, 15650 문제는 중복되는 수열을 제거한 출력값을 요구하고 있다. 즉 재귀 함수를 반복적으로 호출하면서 반복문의 시작점이 한칸씩 증가하면서 진행되어야 한다. 재귀 함수를 호출할 때 인수로 시작점을 지정해준다.
const DFS = (n) =>{
// 배열 길이가 M인 경우 return
if(result.length === M){
console.log(result.join(' '));
return;
}
// 배열을 순회하면서 DFS 돌리기
for(let i=n; i<=N; i++){
if(!result.includes(i)){
result.push(i);
DFS(i+1);
result.pop();
}
}
}
DFS(1);

[Algorithm] treeBFS 알고리즘 Javascript Node.js 구현하기
treeBFS 알고리즘 문제 임의의 트리를 구성하는 노드 중 하나의 Node 객체를 입력받는다. 해당 Node를 시작으로 BFS(Breadth First Search) 알고리즘을 사용해서 전체 트리를 검색한다. 모든 Node의 value를 담
about-tech.tistory.com
[Algorithm] powerSet 알고리즘,문자열 부분 집합 문제 Javascript, Node.js
문제 하나의 집합으로 구성된 문자열을 입력받는다. 각각의 문자를 사용해서 만들 수 있는 모든 부분 집합을 반환하세요. 입력 string 타입, 공백 없는 소문자 알파벳 문자열 출력 배열을 반환한
about-tech.tistory.com
'Algorithm' 카테고리의 다른 글
| [Algorithm] BFS Queue 자바스크립트(primePassword 문제) 구현 (0) | 2022.06.13 |
|---|---|
| [Backtracking] 백준 15651 N과 M 3단계 Node.js 구현하기 (0) | 2022.06.12 |
| [Algorithm] treeBFS 알고리즘 Javascript Node.js 구현하기 (1) | 2022.06.08 |
| [Algorithm] powerSet 알고리즘,문자열 부분 집합 문제 Javascript, Node.js (0) | 2022.06.07 |
| [Algorithm] 퀵 정렬(Quick Sort) Javascript, Node.js 구현하기 (백준 2751 수 정렬하기 2) (0) | 2022.06.05 |





댓글