
Javascript Graph Data Structure
Graph 자료구조는 여러 점들이 복잡하게 연결되어 있는 관계를 표현한 자료구조다.

Graph 자료구조는 정점(Vertex)와 간선(Edge)로 구성된다. 두 정점이 직접적인 관계가 있다면 선으로 연결되고 간접적으로 연결되어 있다면 여러개의 선을 거쳐 연결된다.
Graph 자료구조는 크게 무방향 그래프와 방향 그래프로 구분된다. 한 정점에서 다른 정점으로의 방향이 정해진 경우 반대 방향으로 흐름이 흘러갈 수 없다. 방향 그래프 또한 양방향 간선과 단방향 간선으로 구분된다.

Graph 자료구조 인접행렬
두 정점(Vertex)을 연결하는 간선이 있다는 말은 두 정점이 인접해있다는 것이다. 정점간의 관계를 코드로 표현하기 위해서는 인접행렬을 사용한다. 서로 다른 정점들이 인접한 상태인지를 0과 1을 사용해 2차원 배열로 표현한다.
인접행렬에서도 가중치가 있는 간선이라면 0과 1이 아닌 1 이상의 자연수로 표현될 것이다. 가중치를 계산하는 대표적인 문제는 최단거리를 구하는 문제에서 노드의 최단 거리를 구하는 결과값을 구할 때 가중치 간선을 사용한다.
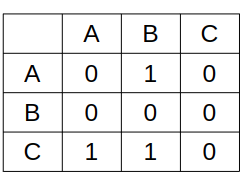
만약 아래 처럼 3개의 정점이 단방향 간선으로 연결되어 있다면 인접행렬은 [3][3] 배열의 인접행렬로 표현할 수 있다.

Graph 자료구조 인접 리스트
인접 리스트는 각 정점이 어떤 정점과 연관되어 있는지를 리스트의 형태로 표현한다. 모든 정점은 하나의 리스트를 가지게 되며, 자신과 인접한 정점을 가지게 된다.
Graph의 인접 리스트는 메모리를 효율적으로 사용해야 하는 경우 사용된다. Graph 자료구조를 표현하는 인접행렬은 Graph 내의 연결가능한 모든 경우의 수를 담고 있기 때문에 많은 메모리를 차지하게 된다. 이 때 인접 리스트의 효용성이 커진다.
Graph 자료구조 가중치 그래프 VS 비가중치 그래프
Graph 자료구조를 가장 많이 사용하는 애플리케이션은 단연 네비게이션이다. 출발점에서 도착점 까지의 최단거리를 계산해서 맵에 표시하기 위해서는 간선간의 가중치를 계산할 수 있어야 한다.
만약 출발점에서 도착점 까지의 간선들이 거리를 표시하고 있지 않다면 최단거리를 구할 수 없다. 이 처럼 간선에 아무런 정보가 기재되어 있지 않은 경우를 비가중치 그래프 라고 한다.

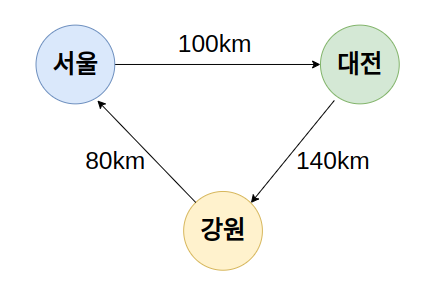
하지만 실제 네비게이션에서는 거리와 도착 시간을 알려주는 기능을 가지고 있다. 이 기능을 구현하기 위해서는 간선간의 단순 인접 정보 뿐만 아니라 거리 정보를 표시해줘야 한다. 이 처럼 간선에서 추가적인 정보를 제공하는 그래프를 가중치 그래프라 한다.
Graph 자료구조 용어들 정리
① 정점(Vertex) : 그래프 자료구조의 기본 요소다. 노드(Node)라고도 불림. 데이터가 저장되는 최소 기준
② 간선(Edge) : 정점간의 관계를 선으로 표시.
③ 인접 정점(Adjacent Vertex) : 정점간 간선으로 연결되어 있는 정점. 연관되어 있는 정점
④ 가중치 그래프(Weighted Graph) : 인접 정보 뿐만 아니라 추가적인 정보를 제공하는 그래프
⑤ 비가중치 그래프(Unweighted Graph) : 인접 정보만 제공하는 그래프
⑥ 무방향 그래프(Undirected Graph) : 인접한 정점간 방향성이 설정되어 있지 않은 그래프
⑦ 진입차수(In-Degree) / 진출차수(Out-Degree) : 특정 정점에 진입하는 간선과 진출하는 간선의 수
⑧ 인접(Adjacency) : 두 정점이 이어져 있는 상태.
⑨ 자기 루프(Self Loop) : 한 정점에서 출발한 간선이 자기자신에게 진입하는 경우. 다른 정점을 거치지 않는다.
⑩ 사이클(Cycle) : 한 정점에서 출발해 자기 자신에게 돌아올 수 있는 경우 사이클이 있다라고 표현한다.
Javascript Graph 자료구조 구현
풀이 :
그래프는 인접행렬로 구현한다. 정점이 한개 추가되면 1차원 배열과 2차원 배열의 length는 동시에 증가한다.
인접행렬에서 간선이 존재한다는 것은 matrix[from_vertex][to_vertex]가 1이라는 것이다.
vertex를 찾는 메소드는 maxtrix[찾고자 하는 vertex] 번째가 존재하는지를 확인하는 것이다.
간선을 추가할 때는 인접행렬의 길이 범위 안에 들어와야 한다. 즉 간선을 추가하고자 하는 vertex는 0보다 크고 인접행렬의 배열의 길이보다 작아야 한다.
간선을 삭제할 때도 인접행렬의 길이 범위안에 들어와야 한다. 0보다 크고 인접행렬의 길이보다 작은 vertex 간의 간선만 삭제가 가능하다.
class Graph {
constructor() {
this.matrix = [];
}
addVertex() {
const currentLength = this.matrix.length;
for (let i = 0; i < currentLength; i++) {
this.matrix[i].push(0);
}
this.matrix.push(new Array(currentLength + 1).fill(0));
}
contains(vertex) {
return this.matrix[vertex] ? true : false;
}
addEdge(from, to) {
const currentLength = this.matrix.length;
if (from === undefined || to === undefined) {
console.log("2개의 인자가 있어야 합니다.");
return;
}
if (from + 1 > currentLength || to + 1 > currentLength || from < 0 || to < 0) {
console.log("범위가 매트릭스 밖에 있습니다.");
return;
}
this.matrix[from][to] = 1;
}
hasEdge(from, to) {
return this.matrix[from][to] === 1;
}
removeEdge(from, to) {
const currentLength = this.matrix.length;
if (from === undefined || to === undefined) {
console.log("2개의 인자가 있어야 합니다.");
return;
}
if (from + 1 > currentLength || to + 1 > currentLength || from < 0 || to < 0) {
console.log("범위가 매트릭스 밖에 있습니다.");
return;
}
this.matrix[from][to] = 0;
}
}
[Algorithm] Data Structure Tree , 트리 자료구조란?
Tree 자료구조란? Tree 자료구조는 나무를 거꾸로 뒤집은 형태로 데이터를 표현하는 자료구조를 의미한다. 그래프의 자료구조 중 단방향 그래프의한 종류다. 한개의 뿌리(Root)로 부터 가지가 사방
about-tech.tistory.com
'Algorithm' 카테고리의 다른 글
| [Algorithm] 순열(Permutation) 경우의 수 구하는 알고리즘 문제(feat. 재귀(Recursion) 함수 사용) (0) | 2022.05.20 |
|---|---|
| [Algorithm] Data Structure Tree , 트리 자료구조란? 이진 탐색 트리 (BST, Binary Search Tree) (0) | 2022.05.16 |
| [Algorithm] Data Structure and Algorithm Stack vs Queue (0) | 2022.05.16 |
| [Algorithm] 조합(Combination)과 순열(Permutation) 알고리즘 Javascript (1) | 2022.05.14 |
| [Algorithm] 하노이의 탑 알고리즘 Javascript 구현하기 (0) | 2022.05.14 |





댓글