
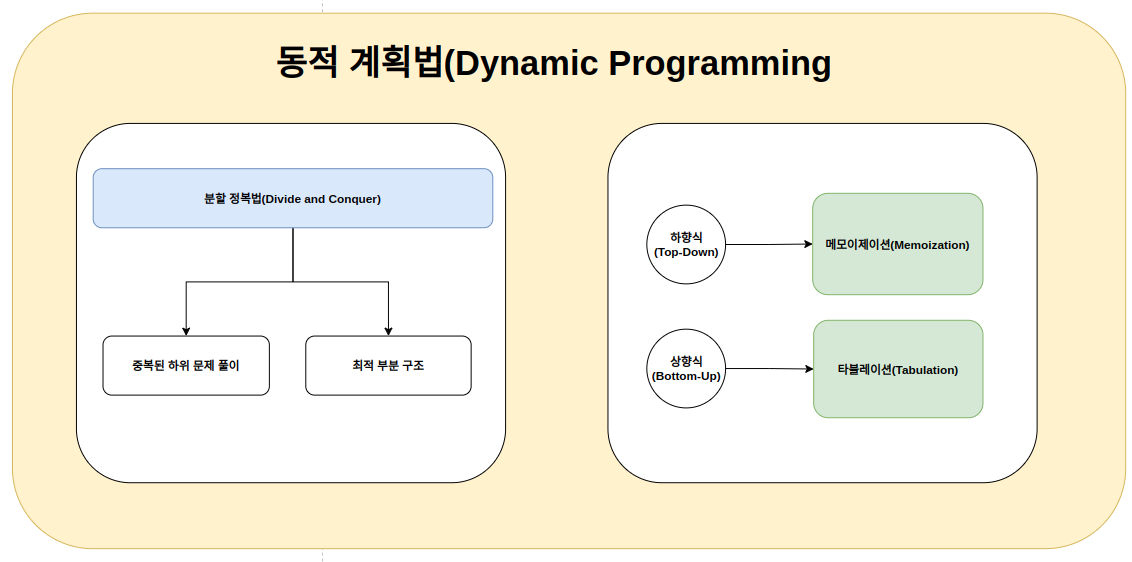
동적 계획법(Dynamic Programming)
동적 계획법은 어떤 문제를 해결하기 위해 그 문제를 더 작은 문제의 연장선으로 생각한다. 가장 하위의 케이스의 해를 구하고 큰 문제의 해를 구해나가는 Bottom-up 방식이다. 쉽게 말해서 이전에 했던 계산을 재활용해서 다음 케이스의 답을 구해나가는 과정이다.
동적 계획법 접근 방식은 큰 그림에서 분할정복법(Divide and Conquer)과 유사하다. 분할정복법 또한 이전에 계산했던 풀이를 재활용해서 새로운 문제의 답을 구해나간다. 동적 계획법은 분할정복법과 달리 이전에 풀었던 풀이를 cache에 저장한 후 다음 케이스의 풀이를 구해나간다. 이 때 사용하는 방법이 메모이제이션(Memoization)이다.
Tiling 알고리즘 문제
문제
세로 길이 2, 가로 길이 n인 2*n의 임의의 보드가 있다. 2 * 1 크기의 타일로 임의의 보드를 채우는 모든 경우의 수를 구하라.
입력값
1 <= n
풀이
만약 n이 1인 경우 보드를 채우는 경우는 1가지다.

만약 n이 2인 경우 보드를 채우는 경우는 2가지다.

만약 n이 3인 경우 보드를 채우는 경우의 수는 3가지다.
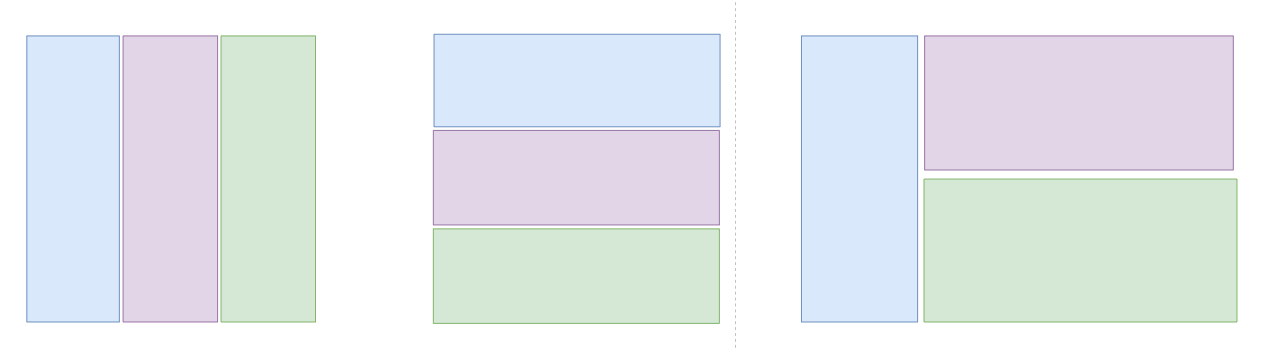
만약 n이 4인 경우 보드를 채우는 경우의 수는 5가지가 존재한다.

결국 가장 작은 경우의 수를 토대로 타일의 길이가 n개추가될 때 마다 경우의 수 또한 규칙적으로 증가한다.
n의 경우의 수 = (n-2)의 경우의 수 + (n-1)의 경우의 수
어디서 많이 본 공식 아닌가? 맞다. 바로 피보나치 수열 공식이다. 다만 n이 1인 경우 2에서 시작한다는 것만 다를 뿐 전체적으로 피보나치 수열 규칙을 가지고 있는 문제다. 답은 간단하게 구할 수 있다.
Basic 타일링 알고리즘 소스코드
let tiling = function (num) {
if(num===1) return 1;
if(num===2) return 2;
return recur(num-1) + recur(num-2);
};
동적 계획법 알고리즘은 기본적으로는 분할 정복과 동일하지만 여기에 문제의 풀이를 최적화 할 수 있는 방법론을 추가한다. 크게 메모이제이션과 타불레이션을 사용한다. 이번 문제에서는 메모이제이션을 사용해서 콜 스택에 추가되는 함수의 갯수를 획기적으로 줄여보자.
cache 오브젝트를 생성하고, 결과값을 cache에 저장한다. cache에 저장된 경우의 수는 더 이상 구할 필요가 없어진다. 피보나치 수열을 구하는 재귀 함수는 콜 스택이 기하급수적으로 증가하기 때문에 둘의 성능을 비교하면 동적 계획법의 성능을 가늠할 수 있다.
동적 계획법 타일링 알고리즘 소스코드
let tiling = function (n) {
const cache = {};
const recur = (num)=> {
if(num in cache) return cache[num]
if(num===1) return 1;
if(num===2) return 2;
cache[num] = recur(num-1) + recur(num-2);
return cache[num];
}
return recur(n);
};
성능 비교
2 * 30 길이의 보드에 타일을 채우는 경우의 수를 구한다.
기본 알고리즘으로 경우의 수를 구할 때 콜 스택에 올라간 함수의 갯수는 1,664,079개가 올라간다.
반면 동적 계획법으로 구현한 알고리즘의 경우 콜 스택 수가 57개 밖에 되지 않는다.
➜ Algorithm_Immerse_Toy node 05_tiling.js
경우의 수 : 1346269;
count_basic : 1664079
count_advanced : 57
[Algorithm] 재귀 알고리즘 배열 javascript 기본 문제 정리
Recursive Algorithm 기초 재귀 알고리즘은 base case 부터 시작한다. 먼저 탈출 조건을 세워놓고, 전체적인 문제를 분해해가면서 함수가 자신을 호출하는 구조를 세부적으로 구성하면서 답을 찾아낸다.
about-tech.tistory.com
[Algorithm] 재귀 알고리즘 문제 Javascript
피보나치 문제 문제 0<= N <= 15 자연수를 입력받아 피보나치 수열의 N 번째 요소를 출력하라 입력 0<= N <= 15 소스코드 function fibonacci(num) { switch(num){ case 0: return 0; case 1: return 1; } return..
about-tech.tistory.com
[Algorithm] Advanced Fibonacci using Memoization
Memoization 함수형 프로그래밍 언어인 Javascript에서 계산 결과를 저장해두는 방식으로 하위 함수를 호출하는 방식이다. 값을 저장할 객체를 생성하고 하위 함수에서 계산된 값을 객체에 저장하면
about-tech.tistory.com
'Algorithm' 카테고리의 다른 글
| [Algorithm] DFS Tree 순회 알고리즘 (0) | 2022.05.30 |
|---|---|
| [Algorithm] SUDOKU Solver 스도쿠 알고리즘 Javascript (0) | 2022.05.29 |
| [Algorithm] 바코드 문제 DFS 알고리즘 기초 Javascript (0) | 2022.05.25 |
| [Algorithm] Advanced Bubble Sort 알고리즘 Javascript (0) | 2022.05.25 |
| [Algorithm] Javascript BFS / DFS 알고리즘 문제 기초 (0) | 2022.05.24 |





댓글