
DFS 트리 순회 알고리즘
DFS 알고리즘으로 트리 구조를 순회하는 문제는 다양하게 활용된다. 트리 구조에서 각 정점을 순회하는 알고리즘은 크게 DFS와 BFS로 구분된다. 루트 노드 부터 단말 노드까지 순회한 뒤 다음 자식 노드를 순회하는 방식이다. BFS 알고리즘은 루트 노드에 연결된 모든 자식노드를 다 순회한 뒤 다음 레벨의 자식노드를 순회한다.
BFS 알고리즘은 최단거리를 구하는 문제에서 사용된다. 현재 연결된 정점을 모두 순회한 뒤 다음 레벨의 정점으로 넘어가는 과정에서 최단거리를 쉽게 구할 수 있기 때문이다. BFS 알고리즘을 구현하는 대표적인 방식은 Queue 자료구조를 이용하는 것이다.
반면 DFS 알고리즘으로 최단거리를 구할 수 있지만 BFS 알고리즘 보다는 더 많은 연산이 필요할 수도 아닐 수도 있다. DFS 알고리즘을 구현하는 방식 중 대표적인 방식이 바로 재귀(Recursion) 방식이다.
문제
임의의 Tree를 구성하는 하나의 Node 객체를 입력받아 해당 노드를 시작으로 깊이 우선 탐색(DFS, Depth First Search)를 진행한다. 탐색되는 노드의 값을 저장한 배열을 반환하라.
입력값
- 'value', 'children' 속성을 가지는 객체(Node)
- 'node.value'는 number 타입 속성
- 'node.children'은 Node를 요소로 가지는 배열 속성
출력값
방문한 노드의 value를 담은 배열
예시
let root = new Node(1);
let rootChild1 = root.addChild(new Node(2));
let rootChild2 = root.addChild(new Node(3));
let leaf1 = rootChild1.addChild(new Node(4));
let leaf2 = rootChild1.addChild(new Node(5));
let output = dfs(root);
console.log(output); // --> [1, 2, 4, 5, 3]
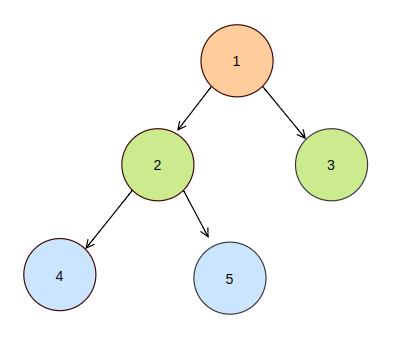
위 예시를 트리 구조로 표현하면 아래 그림이 된다. 루트 노드 1에 2와 3 노드가 추가되고 노드 2에 새로운 노드 4와 5가 추가된다. DFS 알고리즘은 가장 먼저 1 >> 2 >> 4를 검색한다. 이 후 노드 5를 검색한 후 노드 2에 연결된 모든 자식노드 검색을 완료한 뒤에야 노드 3을 검색한다.
소스 코드
① 노드 생성 함수
먼저 추가할 노드를 생성한다. 노드 객체는 value와 children을 속성값으로 가지는 클래스로 생성해준다. 이 후 인스턴스로 생성해서 새로운 노드를 추가한다.
let Node = function (value) {
this.value = value;
this.children = [];
};
위 코드는 아래와 동일하다. Javascript에서 클래스도 결국 function 타입 객체이기 때문에 위와 같이 표현이 가능한 것이다.
class Node{
constructor(value){
this.value = value;
this.children = [];
}
};
② 새로운 노드 추가 함수
노드에 value와 children을 가진 새로운 노드 객체를 추가한다. prototype으로 상속이 이뤄지는 Javascipt에서 새로운 메소드를 추가할 때 prototype을 사용한다.
let Node = function (value) {
this.value = value;
this.children = [];
};
Node.prototype.addChild = function (child) {
this.children.push(child);
return child;
};
위 코드는 아래 코드와 동일하다.
class Node{
constructor(value){
this.value = value;
this.children = [];
}
addChild(child){
this.children.push(child);
return child;
}
};
③ 트리를 순회하는 재귀 함수
노드의 children(배열)을 순회하면서 자식 노드를 검색한다. 만약 자식 노드가 비어있는 경우 현재 노드의 value를 리턴하는 방식으로 루트 노드 부터 단말 노드까지 검색을 진행한다.
let result = [];
if(node.children.length === 0){
return [node.value];
}
result.push(node.value);
for(let i=0; i<node.children.length; i++){
result.push(dfs(node.children[i]))
result = result.flat();
}
return result;
push 함수를 사용하지 않고 concat을 사용해서 간단하게 구현도 가능하다.
let result = [node.value];
node.children.forEach((item, idx)=>{
result = result.concat(dfs(item));
})
return result;
전체 소스 코드
let dfs = function (node) {
return result;
let result = [];
if(node.children.length === 0){
return [node.value];
}
result.push(node.value);
for(let i=0; i<node.children.length; i++){
result.push(dfs(node.children[i]))
result = result.flat();
}
return result;
};
let Node = function (value) {
this.value = value;
this.children = [];
};
Node.prototype.addChild = function (child) {
this.children.push(child);
return child;
};
정리
DFS 알고리즘으로 트리 자료구조를 순회하는 로직 자체는 어렵지 않지만, 복잡한 그래프 및 트리 자료구조를 활용한 문제에 다수 활용되기 때문에 간단한 순회 알고리즘은 그냥 외우고 있는게 편한다.
DFS 알고리즘을 통해 트리를 생성하고 검색하는 로직은 크게 노드생성, 노드 추가, 노드 순회 3가지 파트로 구분된다. 노드는 멤버변수와 메소드를 함께 가지고 있어야 하기에 class로 생성하는게 차후 구현하는 로직을 이용하기 편하다.
[Algorithm] SUDOKU Solver 스도쿠 알고리즘 Javascript
문제 스도쿠(sudoku) 는 9x9 로 이뤄진 퍼즐에 1 부터 9 까지 숫자를 입력하는 게임이다. 조건은 가로줄과 세로줄 그리고 각 9칸의 숫자 중 중복이 있어서는 안된다. 일부 비어있는 칸의 배열을 입력
about-tech.tistory.com
[Algorithm] 바코드 문제 DFS 알고리즘 기초 Javascript
문제 1,2,3 으로만 구성된 수열 바코드를 생성해야 한다. 무조건 1,2,3만 붙여서 바코드를 만들면 쉽겠지만, 조건이 붙어있다. 바코드에서 인접한 두개의 부분 수열이 동일한 경우 바코드로 제작할
about-tech.tistory.com
[Algorithm] Javascript Graph 인접 행렬 길 찾기(BFS 알고리즘 기초 문제)
문제 입력값으로 인접행렬인 2차원 배열과 시작정점(from), 도착정점(to)가 주어진다. from 정점으로 부터 to 정점까지 갈 수 있는 경우의 수가 존재하는지 boolan 값으로 반환하라. 예시 const result = get
about-tech.tistory.com
'Algorithm' 카테고리의 다른 글
| [Algorithm] Binary Search 알고리즘 Javascript (반복, 재귀, 트리구조) (1) | 2022.06.03 |
|---|---|
| [Algorithm] 분할정복 거듭제곱 분할제곱 알고리즘 Javascript (0) | 2022.06.02 |
| [Algorithm] SUDOKU Solver 스도쿠 알고리즘 Javascript (0) | 2022.05.29 |
| [Algorithm] 동적 계획법 타일링 알고리즘 문제 Javascript (0) | 2022.05.26 |
| [Algorithm] 바코드 문제 DFS 알고리즘 기초 Javascript (0) | 2022.05.25 |





댓글