
Tree 자료구조란?
Tree 자료구조는 나무를 거꾸로 뒤집은 형태로 데이터를 표현하는 자료구조를 의미한다. 그래프의 자료구조 중 단방향 그래프의한 종류다. 한개의 뿌리(Root)로 부터 가지가 사방으로 뻣은 형태로 데이터 흐름이 전개된다.
데이터가 아래에 하나 이상의 데이터에 무방향으로 연결되어 있는 계층적인 자료구조의 형태를 가지고 있다. 트리 자료구조는 그래프와 함께 대표적인 비선형 자료구조에 속한다. Tree 자료구조는 계층적으로 표현되고, 아래로만 데이터가 뻗어나가기 때문에 사이클이 존재하지 않는다.
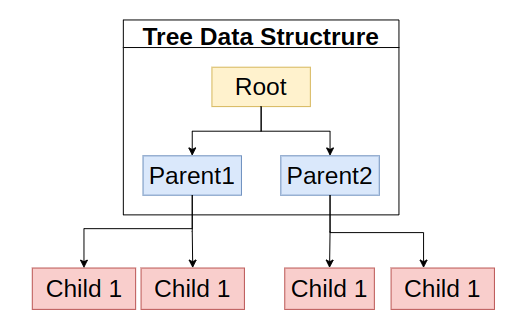
Tree 자료구조는 제일 꼭대기 Node인 루트(Root)에서 시작한다. 아래에 간선으로 연결된 노드(Node)로 구성되어 있따. 노드는 수평관계와 수직관계로 구성되는데 수직관계의 경우 부모/자식 노드가 되고, 자식이 없는 노드는 리프 노드(Leaf Node)라고 한다.
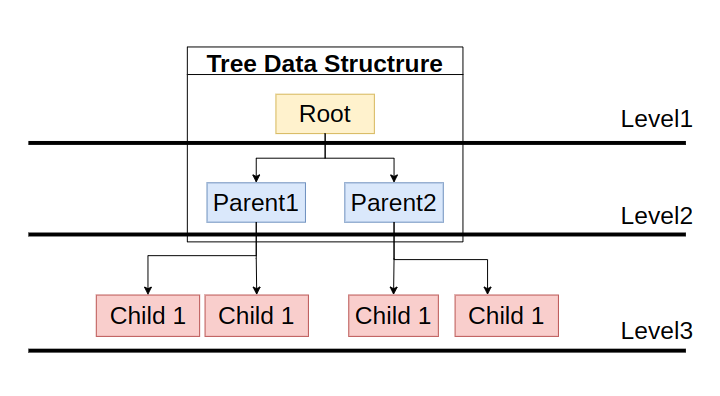
Tree 자료구조는 깊이, 높이, 레벨로 측정이 가능하다.
깊이(Depth)
가장 상위에 위치한 루트(Root) 노드에서부터 특정 노드까지의 깊이를 표현한다. 루트는 깊이가 1이고 부모/자식 노드가 생성될 때마다 깊이가 1씩 증가한다.
레벨(Level)
Tree 자료구조에서 같은 깊이를 가지는 노드들을 묶어서 레벨로 표현한다. 루트 노드 부터 깊이가 0인 경우 레벨 1, 깊이가 1인 경우 레벨 2로 표현한다. 같은 레벨에 존재하는 노드들은 형제노드(Sibling Node)로 표현한다.
높이(Heigth)
가장 마지막에 위치한 노드인 리프 노드(Leaf Node)에서 부터 가장 최상단에 위치한 루트(Root) 노드 까지의 높이를 표현한다. 리프 노드의 높이는 0이며, 부모 노드는 자식노드의 높이 + 1의 값을 가진다.
서브 트리(Sub Tree)
루트(Root) 노드에서 시작하는 큰 트리 구조 안에서 트리 구조를 갖추고 있는 작은 트리를 서브 트리(sub tree)라고 부른다.
Tree 자료구조 용어 정리
① 노드(Node) : 트리 구조를 이루는 개별 데이터
② 루트(Root) : 트리 구조의 시작점
③ 부모 노드(Parent Node) : 두개의 노드가 수직 관계를 가지고 있을 때 루트에 가까운 노드
④ 자식 노드(Child Node) : 두개의 노드가 수직 관계를 가지고 있을 때 리프 노드에 가까운 노드
⑤ 리프 노드(Leaf Node) : 트리 구조의 끝지점. 자식 노드가 없음
Tree 자료구조 활용 이진 탐색 알고리즘(Binary Search Tree)
이진트리(Binary Tree)란 자식 노드가 최대 2개로 구성된 트리 자료구조를 의미한다. 두개의 자식 노드는 왼쪽과 오른쪽 자식노드로 구분된다.
이진트리는 자료 삽입, 삭제 방법에 따라 정 이진 트리(Full Binary Tree), 완전 이진 트리(Complete Binary Tree), 포화 이진 트리(Perfect Binary Tree)로 구분된다.
정 이진 트리(Full Binary Tree)
각 노드가 0개 혹은 2개의 자식 노드를 가진다.
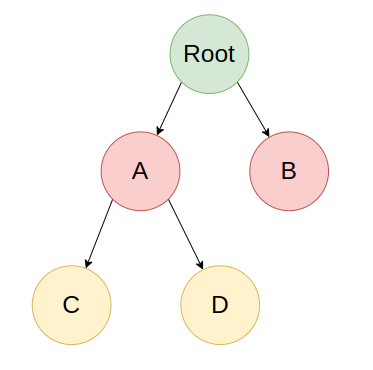
포화 이진 트리(Full Binary Tree)
정 이진 트리의 구조를 가지면서 완전 이진 트리인 경우를 말한다. 리프 노드의 레벨이 동일하면서 모든 레벨이 가득 채워져 있는 상태다.
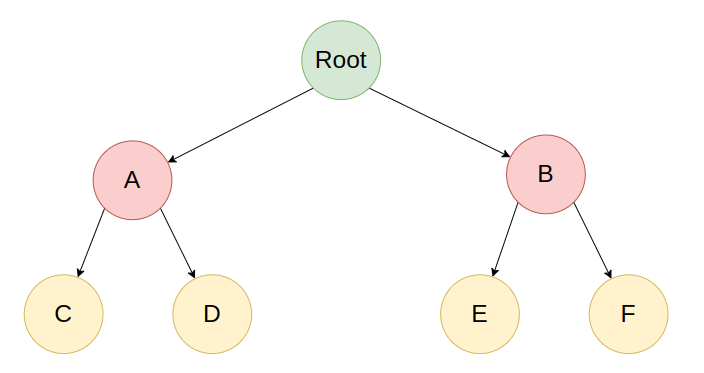
완전 이진 트리(Perfect Binary Tree)
마지막 레벨을 제외한 모든 노드가 가득 차있는 경우다. 마지막 레벨의 노드는 가득 차있지 않아도 되며, 왼쪽은 채워져 있어야 한다.

이진 탐색 트리의 특징
이진 탐색 트리는 왼쪽에 위치한 자식 노드의 값이 부모 노드보다 작다.
오른쪽에 위치한 자식 노드의 값은 부모 노드 보다 크다.
특정 값을 검색할 때 이진 트리 구조로 만들고 검색할 경우 작은 값은 왼쪽에 큰 값은 오른쪽에 위치한다.
하지만 균형잡힌 트리가 아닌 경우 입력되는 값의 순서에 따라서 한쪽으로 노드가 몰리기 때문에 검색 시간(시간 복잡도)가 더 올라가는 경우가 있다.
이진 탐색 트리에서 시간복잡도를 낮추기 위해서는 노드의 삽입과 삭제가 발생할 때 마다 이진 트리의 구조를 재조정하는 과정을 거치는 알고리즘이 추가적으로 필요하다.
이진 탐색 트리(Binary Search Tree , BST) 구현
이진 트리 함수는 insert, contains 메소드를 가진 인스턴스로 구현한다.
클래스의 멤버변수는 노드의 값(Value), left Node, right Node로 구성된다.
이진 탐색 트리는 전위 순회(Preorder), 중위 순회(In-order), 후위 순회(Postorder)로 탐색을 작동한다. 이 경우 callback 함수를 매개변수로 받아 재귀 로직을 구성한다.
① 전위 순회는 Top -> Left > Right 순으로 순회한다. 루트 노드를 가장 먼저 탐색하며 왼쪽의 노드 끝까지 순차적으로 순회한 뒤 오른쪽 노드를 검색한다.
② 중위 순회는 Left -> Top -> Rigth 순으로 순회한다. 제일 왼쪽 끝의 노드(리프 노드) 부터 순회하기 시작해서 루트 노드를 가장 마지막에 탐색한다.
③ 후위 순회는 Left -> Right -> Top 순으로 순회한다. 제일 왼쪽 끝에 있는 노드(리프 노드) 부터 순회하기 시작해서 루트 노드를 가장 마지막에 탐색하게 된다.
class BinarySearchTree {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
// 새로운 Node를 추가하는 메소드
// 값을 비교한 뒤 왼쪽 || 오른쪽으로 노드이동
insert(value) {
if (value < this.value) {
if (this.left === null) {
this.left = new BinarySearchTree(value);
} else {
this.left.insert(value);
}
} else if (value > this.value) {
if (this.right === null) {
this.right = new BinarySearchTree(value);
} else {
this.right.insert(value);
}
}
}
// 트리 내 노드가 존재하는지 확인하는 메소드
contains(value) {
if (this.value === value) {
return true;
}
if (value < this.value) {
if(this.left) return this.left.contains(value)
return false;
}
if (value > this.value) {
if(this.right) return this.right.contains(value)
return false;
}
}
// 전위 순회
// TOP - LEFT - RIGHT
preorder(callback) {
callback(this.value);
if (this.left) {
this.left.preorder(callback);
};
if (this.right) {
this.right.preorder(callback);
};
}
// 중위 순회
// LEFT - TOP - RIGHT
inorder(callback) {
if (this.left) {
this.left.inorder(callback);
};
callback(this.value);
if (this.right) {
this.right.inorder(callback);
};
}
// 후위 순회
// LEFT - RIGHT - TOP
postorder(callback) {
if (this.left) {
this.left.postorder(callback);
};
if (this.right) {
this.right.postorder(callback);
};
callback(this.value);
}
}
[Algorithm] Data Structure Tree , 트리 자료구조란?
Tree 자료구조란? Tree 자료구조는 나무를 거꾸로 뒤집은 형태로 데이터를 표현하는 자료구조를 의미한다. 그래프의 자료구조 중 단방향 그래프의한 종류다. 한개의 뿌리(Root)로 부터 가지가 사방
about-tech.tistory.com
'Algorithm' 카테고리의 다른 글
| [Algorithm] 재귀 알고리즘 문제 Javascript (0) | 2022.05.22 |
|---|---|
| [Algorithm] 순열(Permutation) 경우의 수 구하는 알고리즘 문제(feat. 재귀(Recursion) 함수 사용) (0) | 2022.05.20 |
| [Algorithm] Javascript Graph Data Structure 그래프 자료구조 알고리즘 (1) | 2022.05.16 |
| [Algorithm] Data Structure and Algorithm Stack vs Queue (0) | 2022.05.16 |
| [Algorithm] 조합(Combination)과 순열(Permutation) 알고리즘 Javascript (1) | 2022.05.14 |





댓글