
고속 거듭제곱 구하기
거듭제곱을 구하기 위해서 일반적으로 Math.pow() 함수를 사용하거나 거듭제곱 연산자(**)를 사용한다. 하지만 이 경우 시간 복잡도가 O(n)이기 때문에 거듭제곱해야 할 횟수가 늘어나면 날 수록 엄청난 연산수가 필요하다. 즉, 메모리 활용이 비효율적이게 된다.
거듭제곱을 할 때 고속으로 거듭제곱할 수 있는 방법이 있다. 바로 분할제곱 방법이다. 분할제곱에서는 승수가 홀수일 때와 홀수인 경우로 구분해서 빠르게 거듭제곱을 처리할 수 있다. 예를 들어 2^11을 구한다고 하면 11번의 연산이 반복되어야 한다. 하지만 분할제곱의 경우 3번만에 답을 구할 수 있다.
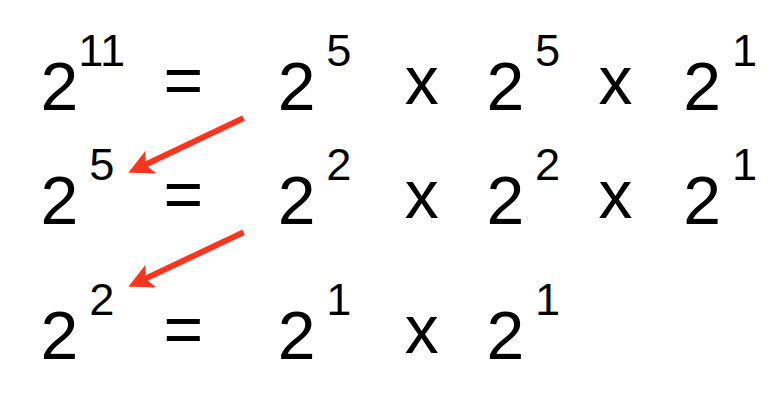
분할제곱 혹은 고속 거듭제곱을 이용할 경우 시간복잡도는 O(Log N)으로 획기적으로 빨라지게 된다. 분할 제곱의 핵심적인 아이디어는 분할 정복법(Divide Conquer)이다. 최종적으로 답을 얻어야 하는 결과를 반씩 분할하면서 답을 구해간다. 지수를 반으로 쪼개면서 홀수와 짝수인 케이스를 처리해준다. 분할 제곱의 공식은 다음과 같다.
N의 k 거듭제곱을 구한다고 했을 때 지수를 반으로 쪼개 가면서 재귀 함수를 호출한다.
- k 가 짝수인 경우 : N^(k/2) * N^(k/2)
- k 가 홀수인 경우 : N^((k-1)/2) * N^((k-1)/2) * N
문제
base와 exponent가 주어질 때 base의 exponent 승의 결과를 구하라.
다만 Math.pow()와 거듭제곱 연산자( ** )은 사용이 금지된다. number 타입을 리턴해야 하고 실제 계산 결과를 94,906,249로 나눈 나머지를 리턴해야 한다. 계산 결과가 컴퓨터로 나타낼 수 있는 수를 넘어설 수 있기 때문이다. 모든 연산을 할 때 마다 나머지를 구하고 그 결과를 연산에 이어나가야 한다.
출력 예시
let result = power(3, 40);
console.log(result); // 19334827
풀이
만약 분할 제곱 방식을 사용하지 않는다면 단단한 코드로 거듭제곱을 구할 수 있다. 만약 power(3,40)이 주어질 때 연산 횟수는 40번이 돌아가야 한다.
function power(base, exponent) {
let result = base;
for(let i=1; i<exponent; i++){
result *= base;
result = result % 94906249;
}
return result;
}
분할제곱 방식으로 결과를 구할 때는 지수를 반으로 분할하면서 재귀 함수를 호출한다. 컴퓨터가 나타낼 수 있는 값의 범위를 지키기 위해 매 연산결과마다 94906249를 나머지 연산을 해준다. 이 경우 power(3,40)을 구할 때 필요한 연산횟수는 7번에 불과하다.
function power(base, exponent) {
// 지수가 0인 경우
if(exponent === 0) return 1;
// 지수가 홀수인 경우
else if(exponent % 2 === 1){
const temp = power(base, (exponent-1)/2) % 94906249;
return (((temp*temp)% 94906249) * base) % 94906249;
}
// 지수가 짝수인 경우
else{
const temp = power(base, (exponent)/2) % 94906249;
return( temp * temp ) % 94906249;
}
}
[Algorithm] DFS Tree 순회 알고리즘
DFS 트리 순회 알고리즘 DFS 알고리즘으로 트리 구조를 순회하는 문제는 다양하게 활용된다. 트리 구조에서 각 정점을 순회하는 알고리즘은 크게 DFS와 BFS로 구분된다. 루트 노드 부터 단말 노드
about-tech.tistory.com
[Algorithm] SUDOKU Solver 스도쿠 알고리즘 Javascript
문제 스도쿠(sudoku) 는 9x9 로 이뤄진 퍼즐에 1 부터 9 까지 숫자를 입력하는 게임이다. 조건은 가로줄과 세로줄 그리고 각 9칸의 숫자 중 중복이 있어서는 안된다. 일부 비어있는 칸의 배열을 입력
about-tech.tistory.com
[Algorithm] 동적 계획법 타일링 알고리즘 문제 Javascript
동적 계획법(Dynamic Programming) 동적 계획법은 어떤 문제를 해결하기 위해 그 문제를 더 작은 문제의 연장선으로 생각한다. 가장 하위의 케이스의 해를 구하고 큰 문제의 해를 구해나가는 Bottom-up
about-tech.tistory.com
'Algorithm' 카테고리의 다른 글
| [Algorithm] 백준 10818번 최소 최대 문제 Node.js 여러줄 입력 받기 (0) | 2022.06.04 |
|---|---|
| [Algorithm] Binary Search 알고리즘 Javascript (반복, 재귀, 트리구조) (1) | 2022.06.03 |
| [Algorithm] DFS Tree 순회 알고리즘 (0) | 2022.05.30 |
| [Algorithm] SUDOKU Solver 스도쿠 알고리즘 Javascript (0) | 2022.05.29 |
| [Algorithm] 동적 계획법 타일링 알고리즘 문제 Javascript (0) | 2022.05.26 |





댓글